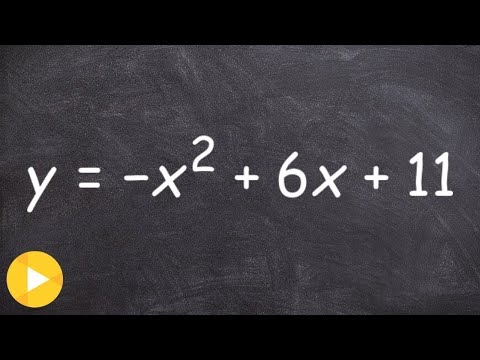When 8850 Form Relating 2016-2024

Welcome, so I have a whole little playlist on how to convert from standard form to vertex form. But I figured I'll just do one little video just so you have an idea, in case you come across some problems where you have to be able to solve or graph, you have to be able to convert from standard form to vertex form. So, I figured I'd make a nice little video for you to do this. So, what we're planning on doing is going from y equals ax squared plus BX plus C and converting that to y equals a times X minus H squared plus K. And you know, there's a lot of reasons why we want to go from standard form to vertex form. A lot of times it's easier to graph, it's very easy to find the vertex and so forth. However, it's not always so simple to convert from one to the other. So, what I did is I'm going to do three examples for you. Now, the main important thing when we look at standard form to vertex form is we notice that vertex form has a binomial squared. And when we take a binomial and we square it, what we get is what we call a perfect square trinomial. Alright, that's what we're going to do, we are going to create what we call a perfect square trinomial, and we're going to do that by what we call the process of completing the square. So, there's going to be a couple of steps, and I'm just going to kind of go through each one individually, and I'm actually going to do it for each problem all together. Now, the first step though we need to do is we need to make sure that...